Gusti Firmansyah: Normal Distributions & Standard Normal Distributions

Distribusi normal adalah keluarga distribusi dengan bentuk lonceng simetris:

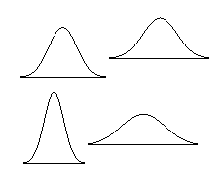
Area di bawah masing-masing kurva di atas adalah sama dan sebagian besar nilai terjadi di tengah kurva. Mean dan standar deviasi dari distribusi normal mengontrol seberapa tinggi dan lebarnya.

Distribusi normal standar (distribusi z) adalah distribusi normal dengan mean 0 dan simpangan baku 1. Setiap titik (x) dari distribusi normal dapat diubah menjadi distribusi normal standar (z) dengan rumus z = ( x-mean) / simpangan baku. z untuk setiap nilai x tertentu menunjukkan berapa banyak standar deviasi x jauh dari rata-rata untuk semua nilai x. Misalnya, jika 1,4m adalah tinggi seorang murid sekolah di mana rata-rata untuk murid usia/jenis kelamin/etnisnya adalah 1,2m dengan standar deviasi 0,4 maka z = (1,4-1,2) / 0,4 = 0,5, yaitu murid adalah setengah standar deviasi dari mean (nilai di pusat kurva).

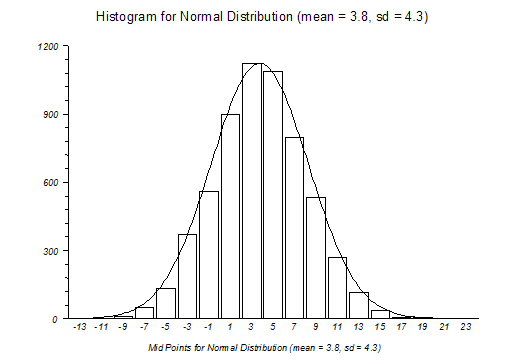
Diagram di atas menunjukkan kurva berbentuk lonceng dari distribusi normal (Gaussian) yang ditumpangkan pada histogram sampel dari distribusi normal. Banyak populasi menunjukkan distribusi normal atau mendekati normal. Ada juga banyak hubungan matematis antara distribusi normal dan distribusi lainnya. Kebanyakan metode statistik membuat "perkiraan normal" ketika sampel cukup besar.

Central Limit Theorem

Untuk memahami mengapa "perkiraan normal" dapat dibuat, pertimbangkan teorema limit pusat. Teorema limit pusat dapat dijelaskan sebagai berikut: Jika Anda mengambil sampel dari suatu populasi dengan beberapa distribusi arbitrer, mean sampel akan, dalam limit, cenderung berdistribusi normal dengan mean yang sama dengan populasi dan dengan varians yang sama dengan varians populasi dibagi dengan ukuran sampel. Oleh karena itu, plot histogram dari rata-rata banyak sampel yang diambil dari satu populasi akan membentuk kurva normal (berbentuk lonceng) terlepas dari distribusi nilai populasi.

Technical Validation

Area ekor dari distribusi normal dievaluasi hingga akurasi 15 desimal menggunakan komplemen dari fungsi kesalahan ( Abramowitz dan Stegun, 1964; Johnson dan Kotz, 1970 ). Kuantil dari distribusi normal dihitung hingga 15 tempat desimal menggunakan metode berdasarkan AS 241 ( Wichura, 1988 ).

z0.001 = -3.09022330616781

Ekor bawah P(z= -3.09022330616781) = 0,001

z0,25 = -0,674489750196082

Ekor bawah P(z= 0.674489750196082) = 0.25

z1E-20 = -9.26234008979841

Ekor bawah P(z= -9.26234008979841) = 9.99999999999962E-21

Dua hasil StatsDirect pertama di atas setuju dengan 15 tempat desimal dengan data referensi Wichura (1988). Nilai ekstrem (P ekor bawah 1E-20) dievaluasi dengan benar hingga 14 tempat desimal.

Definisi Fungsi

Fungsi distribusi, (z), dari variabel normal standar z: